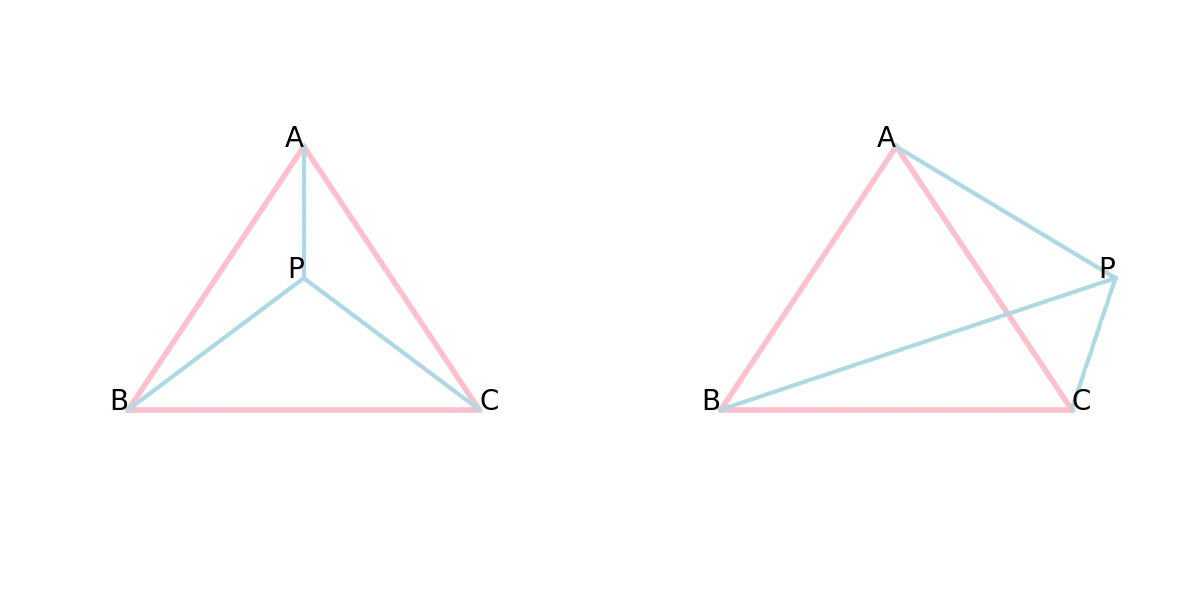
Area Method#

For triangle $\triangle ABC$, if point $p$ is inside or lie on an edge, then the sum of area of $\triangle PAB$, $\triangle PBC$, $\triangle PCA$ should be equivalent to the area of $\triangle ABC$. Otherwise, the sum will be larger.

/***
 * signed area of a triangle connecting points (vert[0], vert[1], vert[2])
 * @param vert vertice of the triangle
 * @return signed area (float)
 */
float area (const std::array<Eigen::Vector2f, 3> vert)
{
		auto const v1 = vert[1] - vert[0];
		auto const v2 = vert[2] - vert[0];
		return 0.5 * (v1.y * v2.x - v1.x * v2.y);
}

/***
 * Area method
 * @param p the point to be checked
 * @param vert vertice of the triangle
 * @return checkmate
 */
bool isInside(const Eigen::Vector2f p, const std::array<Eigen::Vector2f, 3> vert)
{
		auto S = area(vert);
		std::array<Eigen::Vector2f, 3> PAB{p, vert[0], vert[1]};
		auto S1 = area(PAB);
		std::array<Eigen::Vector2f, 3> PBC{p, vert[1], vert[2]};
		auto S2 = area(PBC);
		std::array<Eigen::Vector2f, 3> PCA{p, vert[2], vert[0]};
		auto S3 = area(PCA);
		
		if (fabs(S - S1 - S2- S3) < 10e-9)
				return true;
		return false;
}

Same side method#

For points lying inside a triangle, they must lie on the same side (left or right) for all edges.

/***
 * check whether for all edges, the point lies on the same side
 * @param _p the point to be checked
 * @param _vert vertice of the triangle
 * @return checkmate
 */
bool isInside(const Eigen::Vector2f _p, const std::array<Eigen::Vector2f, 3> _vert)
{
		Eigen::Vector3f vert[3];
		for (int i = 0; i < 3; i++)
		{
				vert[i].x = _vert[i].x;
				vert[i].y = _vert[i].y;
				vert[i].z = 0;
		}
		
		auto AB = vert[1] - vert[0];
		auto BC = vert[2] - vert[1];
		auto CA = vert[0] - vert[2];
		
		Eigen::Vector3f P(_p.x, _p.y, 0);
		auto AP = P - vert[0];
		auto BP = P - vert[1];
		auto CP = P - vert[2];
		
		auto A_nor = AB.cross(AP);
		auto B_nor = BC.cross(BP);
		auto C_nor = CA.cross(CP);
		
		if (A_nor.dot(B_nor) > 0 && B_nor.dot(C_nor) > 0 && C_nor.dot(A_nor) > 0)
				return true;
		return false;
}

Barycentric Coordinates Method#

For triangle $\triangle ABC$ and point $P$, we can express $P$ in the following form:

and the iff. condition where $P$ lies inside $\triangle ABC$ is

We can calculate that

That’s all. I shall implement the code if I use it in the future.

Vector Cross Product Method#

This method is related with winding number. If you walk along the triangle by edges in counter-clockwise direction, from the insight of inside point, the direction is consistent, and the outside point is opposite. That is to say, the winding number of the former is 1, and the latter is 0.

As for the direction of walk, it can expressed as $\overrightarrow{PA}\times \overrightarrow{PB}$, $\overrightarrow{PB}\times \overrightarrow{PC}$and $\overrightarrow{PC}\times \overrightarrow{PA}$, equivalent to the direction of angular velocity.

/***
 * check whether for all edges, the point lies on the same side
 * @param _p the point to be checked
 * @param _vert vertice of the triangle
 * @return checkmate
 */
bool isInside(const Eigen::Vector2f _p, const std::array<Eigen::Vector2f, 3> _vert)
{
		Eigen::Vector3f vert[3];
		for (int i = 0; i < 3; i++)
		{
				vert[i].x = _vert[i].x;
				vert[i].y = _vert[i].y;
				vert[i].z = 0;
		}
		
		Eigen::Vector3f P(_p.x, _p.y, 0);
		auto PA = vert[0] - P;
		auto PB = vert[1] - P;
		auto PC = vert[2] - P;
		
		auto omega1 = PA.cross(PB);
		auto omega2 = PB.cross(PC);
		auto omega3 = PC.cross(PA);
		
		if (omega1.dot(omega2) > 0 && omega2.dot(omega3) > 0 && omega3.dot(omega1) > 0)
				return true;
		return false;
}

Algorithm efficiency#

4>3>2>1. Meet the natural intuition about the number of instruction of different functions.